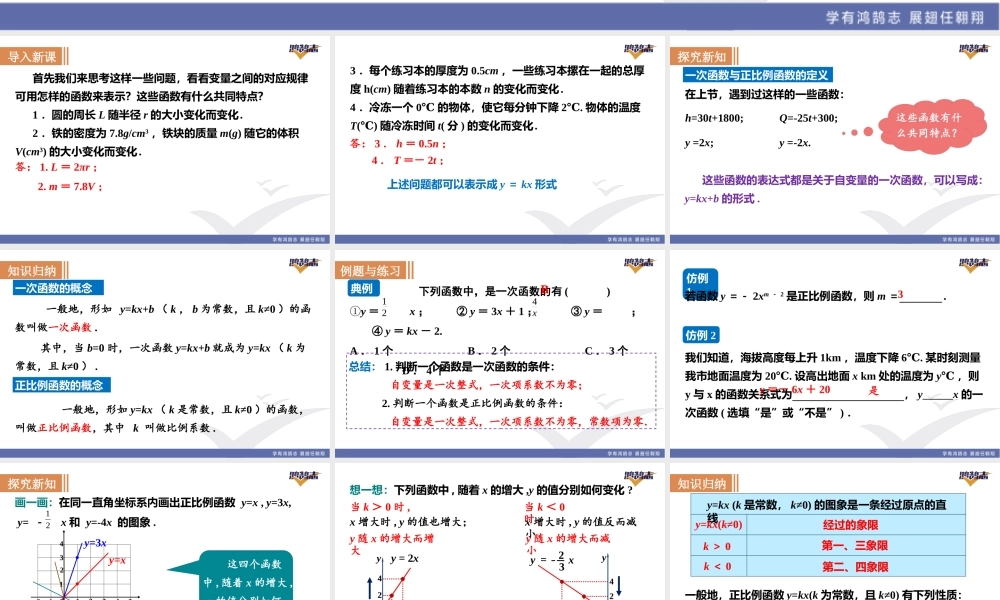
第十二章一次函数12.2一次函数第1课时正比例函数的图象性质导入新课首先我们来思考这样一些问题,看看变量之间的对应规律可用怎样的函数来表示?这些函数有什么共同特点?1.圆的周长L随半径r的大小变化而变化.2.铁的密度为7.8g/cm3,铁块的质量m(g)随它的体积V(cm3)的大小变化而变化.答:1.L=2πr;2.m=7.8V;3.每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(cm)随着练习本的本数n的变化而变化.4.冷冻一个0℃的物体,使它每分钟下降2.℃物体的温度T()℃随冷冻时间t(分)的变化而变化.答:3.h=0.5n;4.T=-2t;上述问题都可以表示成y=kx形式探究新知一次函数与正比例函数的定义在上节,遇到过这样的一些函数:h=30t+1800;Q=-25t+300;y=2x;y=-2x.这些函数有什么共同特点?这些函数的表达式都是关于自变量的一次函数,可以写成:y=kx+b的形式.一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数.其中,当b=0时,一次函数y=kx+b就成为y=kx(k为常数,且k≠0).知识归纳一般地,形如y=kx(k是常数,且k≠0)的函数,叫做正比例函数,其中k叫做比例系数.一次函数的概念正比例函数的概念例题与练习典例下列函数中,是一次函数的有()①y=x;②y=3x+1;③y=;④y=kx-2.A.1个B.2个C.3个D.4个124xB总结:1.判断一个函数是一次函数的条件:自变量是一次整式,一次项系数不为零;2.判断一个函数是正比例函数的条件:自变量是一次整式,一次项系数不为零,常数项为零.仿例1若函数y=-2xm-2是正比例函数,则m=.3仿例2我们知道,海拔高度每上升1km,温度下降6.℃某时刻测量我市地面温度为20.℃设高出地面xkm处的温度为y℃,则y与x的函数关系式为,yx的一次函数(选填“是”或“不是”).y=-6x+20是画一画:在同一直角坐标系内画出正比例函数y=x,y=3x,y=-x和y=-4x的图象.21这四个函数中,随着x的增大,y的值分别如何变化?探究新知12345-1-2o1234-1-2-3-4y=3xy=xy=-4xy=-x12当k>0时,x增大时,y的值也增大;当k<0时,x增大时,y的值反而减小.xy024y=2x1224y随x的增大而增大y随x的增大而减小y=x32-3-6xy0想一想:下列函数中,随着x的增大,y的值分别如何变化?知识归纳y=kx(k是常数,k≠0)的图象是一条经过原点的直线y=kx(k≠0)k>0k<0经过的象限第一、三象限第二、四象限一般地,正比例函数y=kx(k为常数,且k≠0)有下列性质:当k>0时,y随x的增大而增大(图象是自左向右上升的);当k<0时,y随x的增大而减小(图象是...