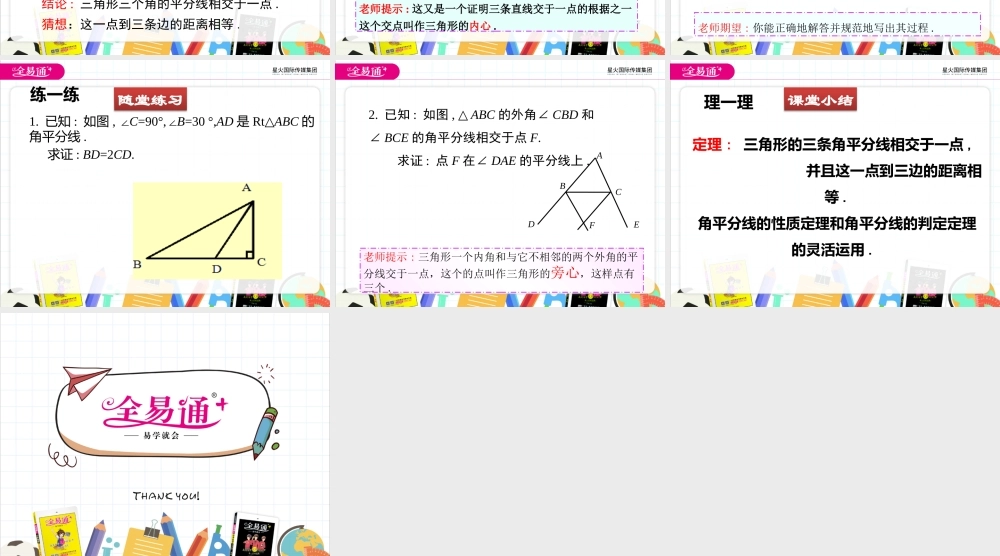
第一章三角形的证明4角平分线(第2课时)学习目标1.能够证明三角形的三条角平分线交于一点且这一点到三条边的距离相等.2.角平分线的性质定理和判定定理的灵活运用.1.角平分线的性质定理角平分线上的点到这个角的两边距离相等.CB1A2PDEO复习旧知∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E,∴PD=PE.2.角平分线的判定定理在一个角的内部,且到角的两边距离相等的点在这个角的平分线上.∵PD⊥OA,PE⊥OB,垂足分别是D,E,且PD=PE,∴点P在∠AOB的平分线上.CB1A2PDEO剪一个三角形纸片通过折叠找出每个角的平分线.观察这三条角平分线,你发现了什么?结论:三角形三个角的平分线相交于一点.动一动猜想:这一点到三条边的距离相等.讲授新课已知:如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D.求证:∠BAC的平分线经过点P,且PD=PE=PF..证一证PDEFABCMN定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.如图,在△ABC中,∵BM,CN,AH分别是△ABC的三条角平分线,且PD⊥AB,PE⊥BC,PF⊥AC(已知),∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫作三角形的内心.ABCPMNDEF例如图,在△ABC中,已知AC=BC,∠C=90°,AD是△ABC的角平线,DE⊥AB,垂足为E.(1)如果CD=4cm,求AC的长;(2)求证:AB=AC+CD.用一用老师期望:你能正确地解答并规范地写出其过程.例题讲解练一练1.已知:如图,∠C=90°,∠B=30°,AD是Rt△ABC的角平分线.求证:BD=2CD.随堂练习2.已知:如图,△ABC的外角∠CBD和∠BCE的角平分线相交于点F.求证:点F在∠DAE的平分线上.ABCFDE老师提示:三角形一个内角和与它不相邻的两个外角的平分线交于一点,这个的点叫作三角形的旁心,这样点有三个.理一理定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.角平分线的性质定理和角平分线的判定定理的灵活运用.课堂小结