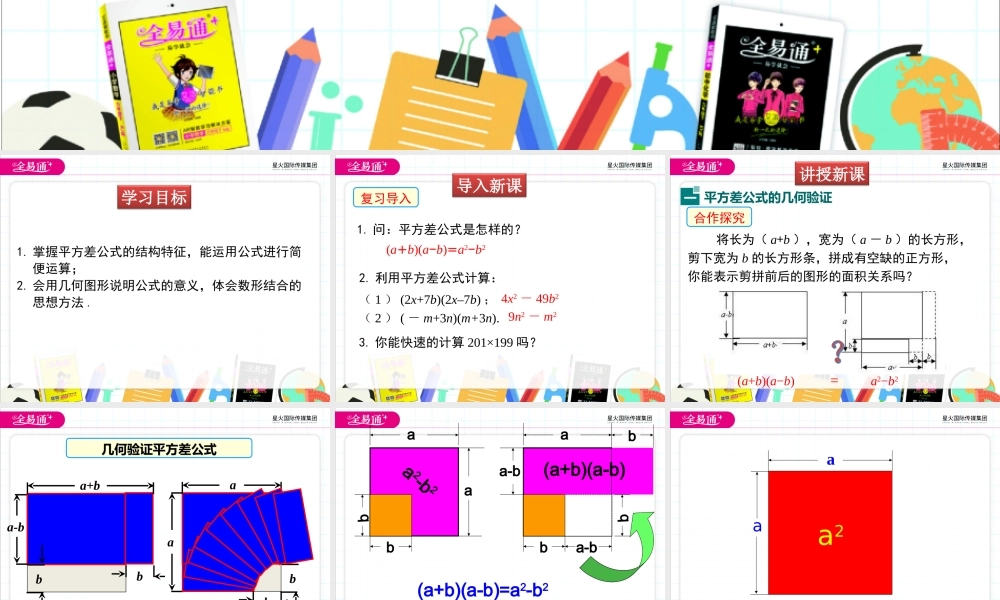
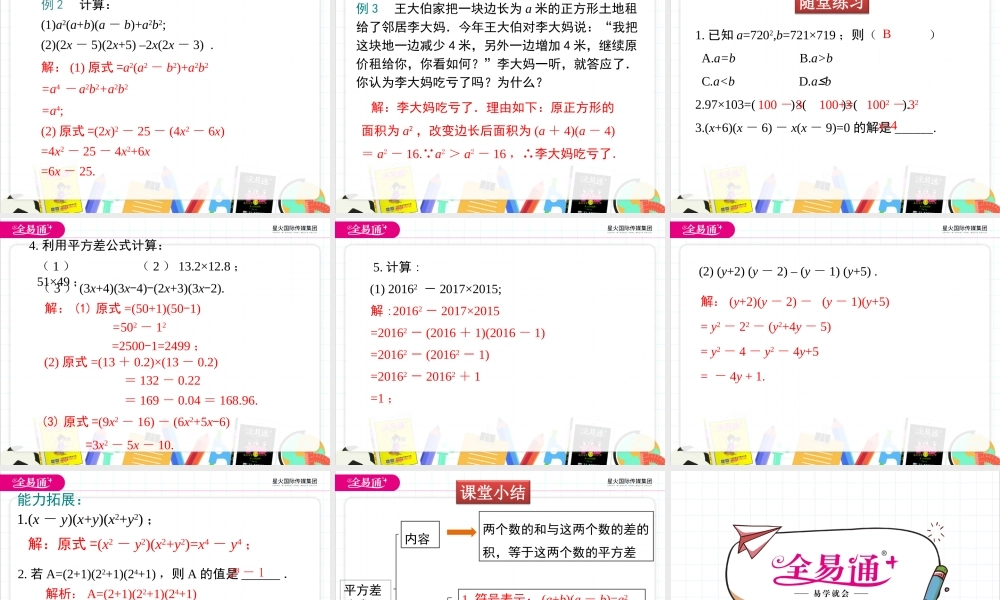
第一章整式的乘除5平方差公式(第2课时)1.掌握平方差公式的结构特征,能运用公式进行简便运算;2.会用几何图形说明公式的意义,体会数形结合的思想方法.学习目标复习导入1.问:平方差公式是怎样的?(a+b)(a−b)=a2−b22.利用平方差公式计算:(1)(2x+7b)(2x–7b);(2)(-m+3n)(m+3n).3.你能快速的计算201×199吗?4x2-49b29n2-m2导入新课将长为(a+b),宽为(a-b)的长方形,剪下宽为b的长方形条,拼成有空缺的正方形,你能表示剪拼前后的图形的面积关系吗?(a+b)(a−b)=a2−b2一平方差公式的几何验证合作探究讲授新课aabba+ba-bbb22))((bababa几何验证平方差公式aabba2-b2abbb(a+b)(a-b)(a+b)(a-b)=a2-b2a-ba-baaa2baa2-b2abbaab12(a+b)(a-b)12(a+b)(a-b)baab(a+b)(a-b)=a2-b2自主探究想一想:(1)计算下列各式,并观察他们的共同特点:6×8=4814×16=22469×71=48997×7=4915×15=22570×70=4900平方差公式的运用二(2)从以上的过程中,你发现了什么规律?请用字母表示这一规律,你能说明它的正确性吗?(a+b)(a−b)=a2−b2典例精析例1计算:(1)103×97;(2)118×122.解:103×97=(100+3)(100-3)=1002-32=10000–9=9991;解:118×122=(120-2)(120+2)=1202-22=14400-4=14396.注意:不能直接应用公式的,要经过变形才可以应用例2计算:(1)a2(a+b)(a-b)+a2b2;(2)(2x-5)(2x+5)–2x(2x-3).解:(1)原式=a2(a2-b2)+a2b2=a4-a2b2+a2b2=a4;(2)原式=(2x)2-25-(4x2-6x)=4x2-25-4x2+6x=6x-25.例3王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续原价租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?解:李大妈吃亏了.理由如下:原正方形的面积为a2,改变边长后面积为(a+4)(a-4)=a2-16. a2>a2-16,∴李大妈吃亏了.1.已知a=7202,b=721×719;则()A.a=bB.a>bC.a