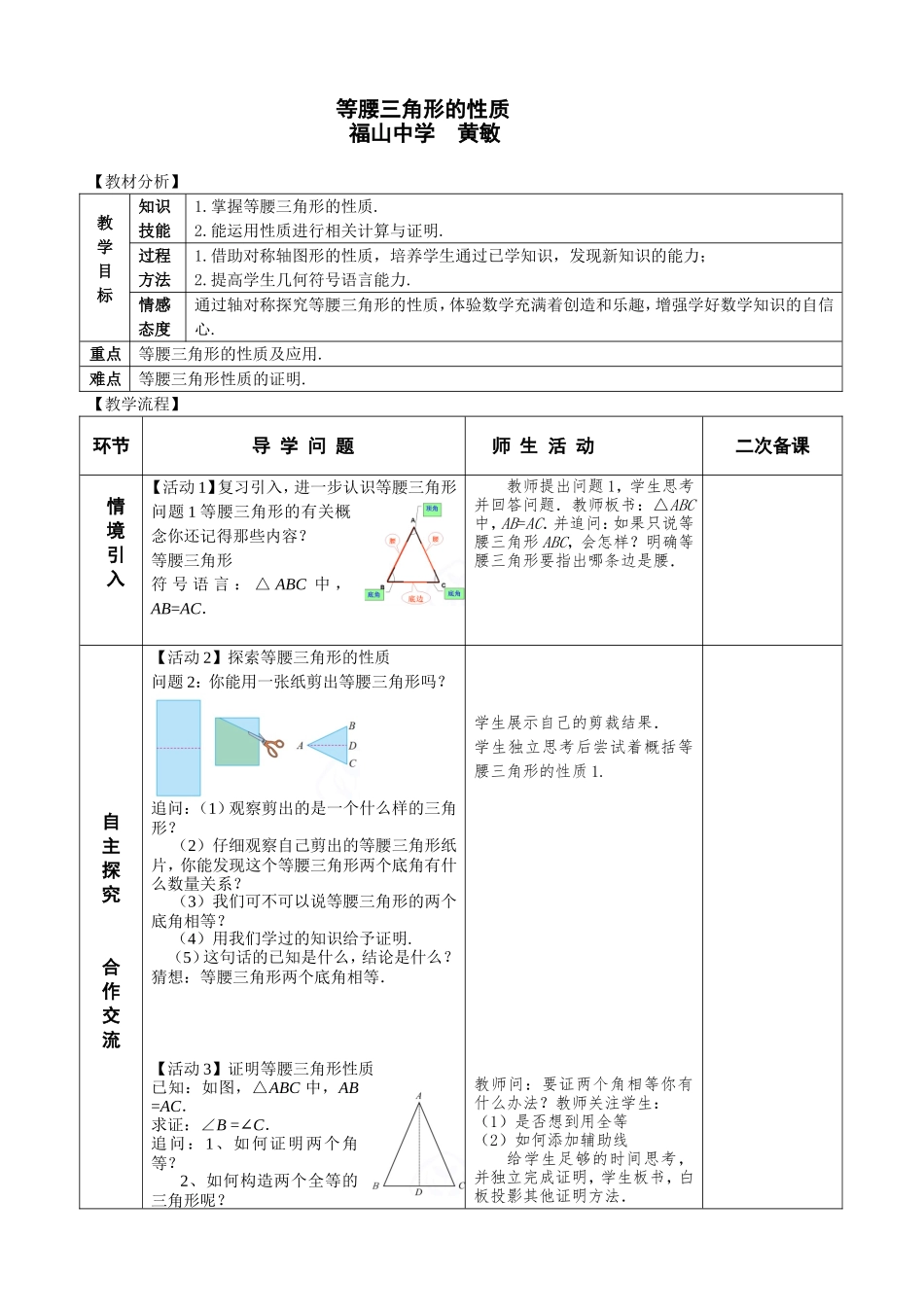
等腰三角形的性质福山中学黄敏【教材分析】教学目标知识技能1.掌握等腰三角形的性质.2.能运用性质进行相关计算与证明.过程方法1.借助对称轴图形的性质,培养学生通过已学知识,发现新知识的能力;2.提高学生几何符号语言能力.情感态度通过轴对称探究等腰三角形的性质,体验数学充满着创造和乐趣,增强学好数学知识的自信心.重点等腰三角形的性质及应用.难点等腰三角形性质的证明.【教学流程】环节导学问题师生活动二次备课情境引入【活动1】复习引入,进一步认识等腰三角形问题1等腰三角形的有关概念你还记得那些内容?等腰三角形符号语言:△ABC中,AB=AC.教师提出问题1,学生思考并回答问题.教师板书:△ABC中,AB=AC.并追问:如果只说等腰三角形ABC,会怎样?明确等腰三角形要指出哪条边是腰.自主探究合作交流【活动2】探索等腰三角形的性质问题2:你能用一张纸剪出等腰三角形吗?追问:(1)观察剪出的是一个什么样的三角形?(2)仔细观察自己剪出的等腰三角形纸片,你能发现这个等腰三角形两个底角有什么数量关系?(3)我们可不可以说等腰三角形的两个底角相等?(4)用我们学过的知识给予证明.(5)这句话的已知是什么,结论是什么?猜想:等腰三角形两个底角相等.【活动3】证明等腰三角形性质已知:如图,△ABC中,AB=AC.求证:∠B=∠C.追问:1、如何证明两个角等?2、如何构造两个全等的三角形呢?学生展示自己的剪裁结果.学生独立思考后尝试着概括等腰三角形的性质1.教师问:要证两个角相等你有什么办法?教师关注学生:(1)是否想到用全等(2)如何添加辅助线给学生足够的时间思考,并独立完成证明,学生板书,白板投影其他证明方法.自主探究合作交流3、刚刚折纸给你什么启示?证明:作底边的中线AD.∴BD=BC在△ABD和△ACD中AB=AC, BD=CD,AD=AD,∴△ABD≌△ACD(SSS).∴∠B=∠C(全等三角形对应角相等).追问:还有没有其他证明方法性质1:等腰三角形两个底角相等.(简写成“等边对等角”)符号语言: △ABC中,AB=AC∴∠B=∠C【活动4】再看自己剪好的等腰三角形,重点看折痕,你有新的发现?性质2:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合.(简写成“三线合一”)在△ABC中(1) AB=AC,AD⊥BC,∴∠___=∠___,____=____;(2) AB=AC,AD是中线,∴∠_=∠_,____⊥____;(3) AB=AC,AD是角平分线,∴____⊥____,____=____.[例1]如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求...