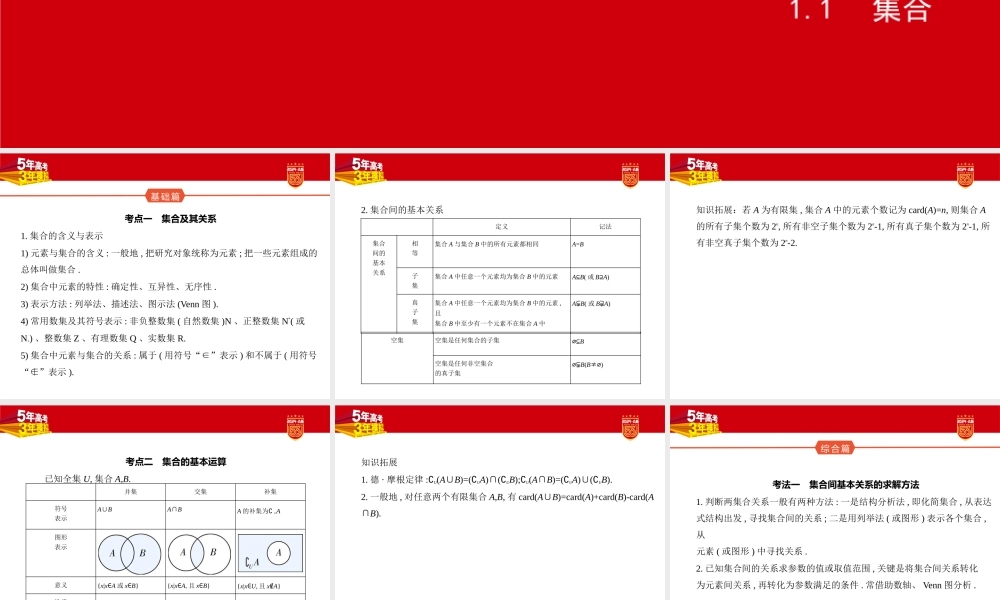
高考数学专题一集合与常用逻辑用语1.1集合基础篇考点一集合及其关系1.集合的含义与表示1)元素与集合的含义:一般地,把研究对象统称为元素;把一些元素组成的总体叫做集合.2)集合中元素的特性:确定性、互异性、无序性.3)表示方法:列举法、描述法、图示法(Venn图).4)常用数集及其符号表示:非负整数集(自然数集)N、正整数集N*(或N+)、整数集Z、有理数集Q、实数集R.5)集合中元素与集合的关系:属于(用符号“∈”表示)和不属于(用符号“∉”表示).2.集合间的基本关系定义记法集合间的基本关系相等集合A与集合B中的所有元素都相同A=B子集集合A中任意一个元素均为集合B中的元素A⊆B(或B⊇A)真子集集合A中任意一个元素均为集合B中的元素,且集合B中至少有一个元素不在集合A中A⫋B(或B⫌A)空集空集是任何集合的子集⌀⊆B空集是任何非空集合的真子集⌀⫋B(B≠⌀)知识拓展:若A为有限集,集合A中的元素个数记为card(A)=n,则集合A的所有子集个数为2n,所有非空子集个数为2n-1,所有真子集个数为2n-1,所有非空真子集个数为2n-2.考点二集合的基本运算已知全集U,集合A,B.并集交集补集符号表示A∪BA∩BA的补集为∁UA图形表示意义{x|x∈A或x∈B}{x|x∈A,且x∈B}{x|x∈U,且x∉A}性质A∪⌀=A;A∪A=A;A∪B=B∪A;A∪B=A⇔B⊆AA∩⌀=⌀;A∩A=A;A∩B=B∩A;A∩B=A⇔A⊆BA∪(∁UA)=U;A∩(∁UA)=⌀;∁U(∁UA)=A知识拓展1.德·摩根定律:∁U(A∪B)=(∁UA)∩(∁UB);∁U(A∩B)=(∁UA)∪(∁UB).2.一般地,对任意两个有限集合A,B,有card(A∪B)=card(A)+card(B)-card(A∩B).综合篇考法一集合间基本关系的求解方法1.判断两集合关系一般有两种方法:一是结构分析法,即化简集合,从表达式结构出发,寻找集合间的关系;二是用列举法(或图形)表示各个集合,从元素(或图形)中寻找关系.2.已知集合间的关系求参数的值或取值范围,关键是将集合间关系转化为元素间关系,再转化为参数满足的条件.常借助数轴、Venn图分析.例1(2022浙江温州4月检测,10)设集合A={x|-3≤x≤2},B={x|k-1≤x≤2k+1},且A⊇B,则实数k的取值范围是(写成集合的形式).解析由B⊆A知,B=⌀或B为A的非空子集.①当集合B≠⌀时,解得-2≤k≤;②当集合B=⌀时,有k-1>2k+1,解得k<-2.综上,可知k≤,故实数k的取值范围为kk≤.13,212,121,kkkk121212答案kk≤12名师点睛根据集合间的关系求参数的值(或取值范围)应注意:(1)两个转化:A∩B=A⇔A⊆B;A∪B=A⇔B⊆A.(2)空集的特殊性.①若B⊆A,则分B=⌀和B≠⌀两类进行讨论.②若A∩B=⌀...