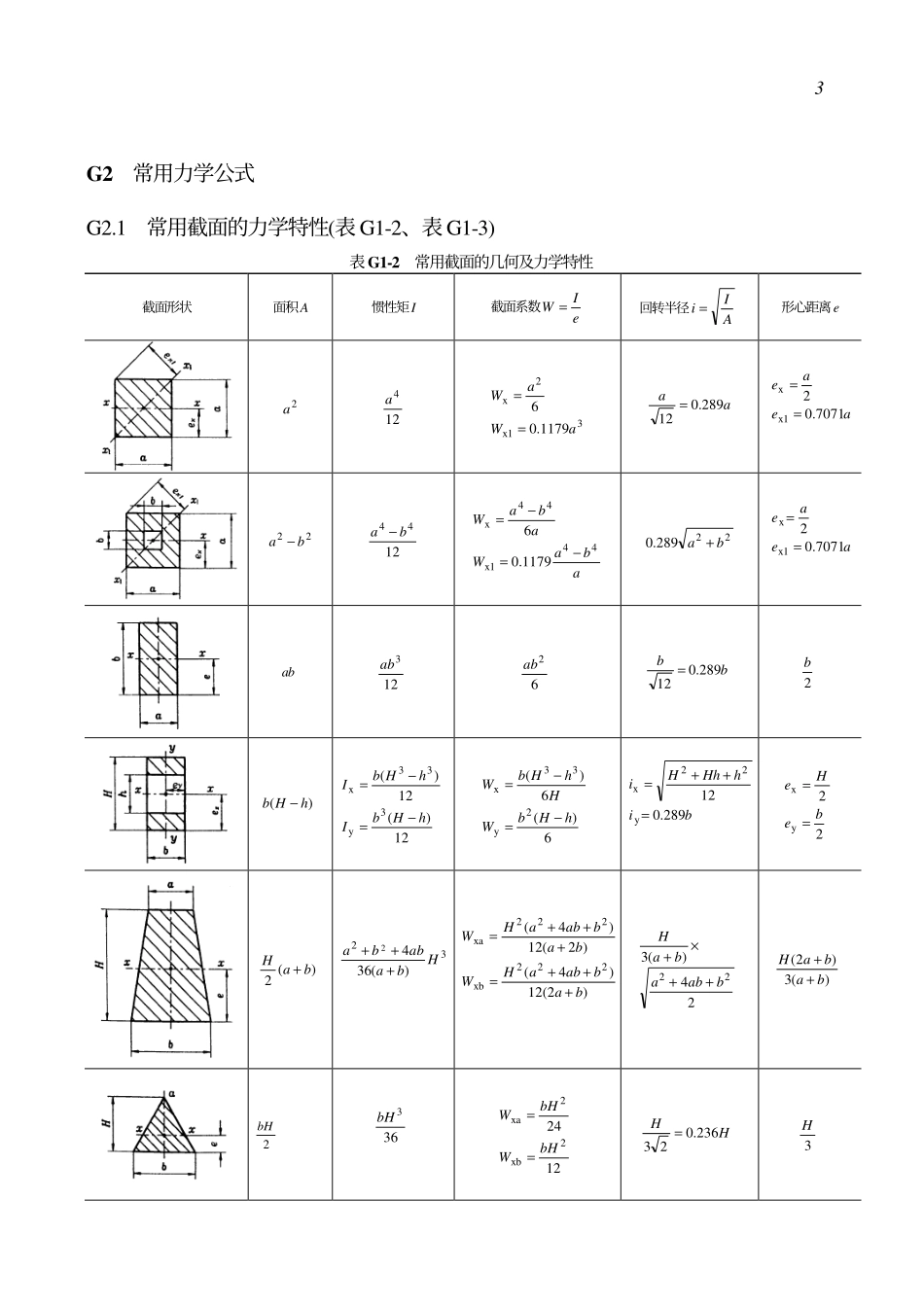
第1章常用资料、数据和一般标准G1常用几何体的体积、面积及重心位置(表G1-1)表G1-1常用几何体的体积、面积及重心位置图形体积V、底面积A、侧面积A0、全面积An、重心位置G的计算公式图形体积V、底面积A、侧面积A0、全面积An、重心位置G的计算公式2)(364G2n2023aZdadaAaAaAaV======为对角线)3(4)4()2(p)2(p)(pp2p)3(3p)3(6pG222n2202222hrhrhZaharhAharhAaAhrhhahV−−=+=+=+===−=+=2)()(2)(2G222n0hZdhbadbhahabAbahAabAabhV=++=++=+===为对角线在椭球中心重心GabcVp34=与球心重合重心GrArV2n3p4p34==在圆环中心重心GDdRrADdRrV22n2222pp44pp2====rZrArArArV83p3p2pp32G2n2023=====V=πr2hA0=2πrhAn=2πr(r+h)ZG=2h2(续)图形体积V、底面积A、侧面积A0、全面积An、重心位置G的计算公式图形体积V、底面积A、侧面积A0、全面积An、重心位置G的计算公式2))((p2)(p2)(p)(pGn02222hZhrRrRArRhArRArRhV=+−+=+=−=−=)22(2)3(])(4)()(4)[(21)22(611111111G01n2121212101111111babaababbabaababhZAAAAbbhaaaahbbAabAbaAbabaababhV++++++=++=−+++−++===+++=)(4)32()()(p)(p)(3p2222G22022n022rRrRrRrRhZhrRlArRArRlARrrRhV++++=+−=++=+=++=44232332331G0n22022hZAAAalaAaAhaAhV=+=−====4)(pppp31G22n022hZhrllrrArlArAhrV=+=+====)()(4)32()(3233233131212212G01n10221211111为斜高为顶面积,gAaaaaaaaahZAAAAaagAaAaAaaaahAV++++=++=+===����������������++=4)44(21)44(2131G2222n22220hZbhaahbabAbhaahbAabAabhV=++++=+++===2)(46336233233G222n022hZdahdahaAahAaAhaV=+=+====为对角线3G2常用力学公式G2.1常用截面的力学特性(表G1-2、表G1-3)表G1-2常用截面的几何及力学特性截面形状面积A惯性矩I截面系数eIW=回转半径AIi=形心距离e2a124a3x12x1179.06aWaW==aa289.012=aeae7071.02x1x==22ba−1244ba−abaWabaW44x144x1179.06−=−=22289.0ba+aeae7071.02x1x==ab123ab62abbb289.012=2b)(hHb−12)(12)(3y33xhHbIhHbI−=−=6)(6)(2y33xhHbWHhHbW−=−=bihHhHi289.012y22x=++=22yxbeHe==)(2baH+32)(3642Hbaabba+++)2(12)4()2(12)4(222xb222xabababaHWbababaHW+++=+++=24)(322bababaH++×+)(3)2(babaH++2bH363bH12242xb2xabHWbHW==HH236.023=3H4(续)截面形状面积A惯性矩I截面系数eIW=回转半径AIi=形心距离eRCCA==2598.2xyxIIRI==45413.03y3x5413.0625.0RWRW==Ri4566.0x=ReRe==yx866.04p2d64p4d32p3d4d2d)(4p22dD−)(64p44dD−������...