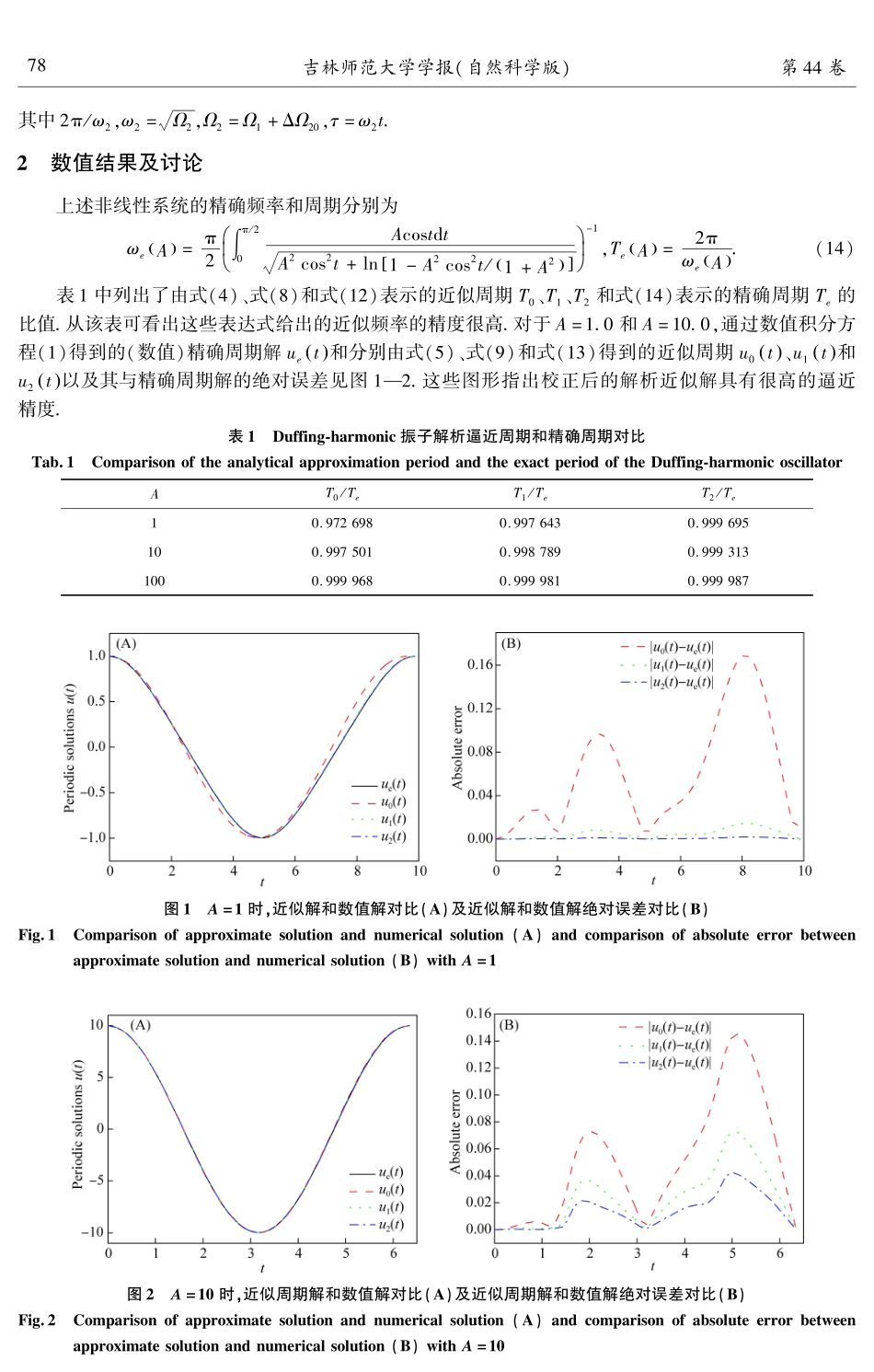
第44卷第3期吉林师范大学学报(自然科学版)Vol.44ꎬNo.32023年8月JournalofJilinNormalUniversity(NaturalScienceEdition)Aug.ꎬ2023收稿日期:2023 ̄06 ̄31基金项目:国家自然科学基金项目(11672118)ꎻ吉林省自然科学基金项目(YDZJ202301ZYTS391)第一作者简介:刘伟佳(1988—)ꎬ女ꎬ吉林省四平市人ꎬ讲师ꎬ博士.研究方向:非线性振动.doi:10.16862/j.cnki.issn1674 ̄3873.2023.03.012Duffing ̄harmonic振子预估 ̄校正谐波平衡法求解刘伟佳ꎬ张与同(吉林师范大学数学与计算机学院ꎬ吉林四平136000)摘要:利用预估 ̄校正谐波平衡方法求解Duffing ̄harmonic振子ꎬ建立了系统的解析近似周期与周期解.所得近似解与由数值方法计算得到的精确解比具有高精度.结果表明ꎬ预估 ̄校正谐波平衡方法在求解强非线性系统时ꎬ是一种行之有效的方法.关键词:Duffing ̄harmonic振子ꎻ预估 ̄校正谐波平衡法ꎻ近似解中图分类号:O322文献标志码:A文章编号:1674 ̄3873 ̄(2023)03 ̄0076 ̄040引言自然界和工程技术中的动力学现象本质上都是非线性的ꎬ为了方便解释各种非线性现象的物理本质和解决工程中的非线性振动问题ꎬ非线性振动分析与计算方法的研究就显得尤为重要[1 ̄3].考虑恢复力以有理形式表示的Duffing ̄harmonic振子d2udt2+u31+u2=0ꎬu0()=Aꎬdudt0()=0.(1)近年来多位学者用不同的方法对该振子进行了研究ꎬ如:谐波平衡法[4 ̄7]、平均法[8]、迭代法[9]、同伦分析法[10]等.谐波平衡法的突出特点是不要求所求解的非线性振动问题的非线性项是小量但难以构造更高精度的近似解.根据上述问题ꎬB.S.Wu等[11]基于预估 ̄校正的思想ꎬ结合牛顿法对谐波平衡法进行改进.本文用预估 ̄校正谐波平衡法求解了方程(1)ꎬ仅应用一次预估 ̄校正迭代便可得到显式的、简洁的、高精度近似周期与周期解ꎬ表明该方法求解强非线性振子的有效性.1预估 ̄校正谐波平衡法将式(1)变形ꎬ并引进新的变量τ=ωtꎬ得Ω1+u2()u¨+u3=0ꎬu0()=Aꎬu0()=0.(2)其中Ω=ω2ꎬ符号圆点表示对τ的微分.选择这个新的独立变量可使方程(2)的解为一个关于τ的周期为2π的周期函数ꎬ非线性...