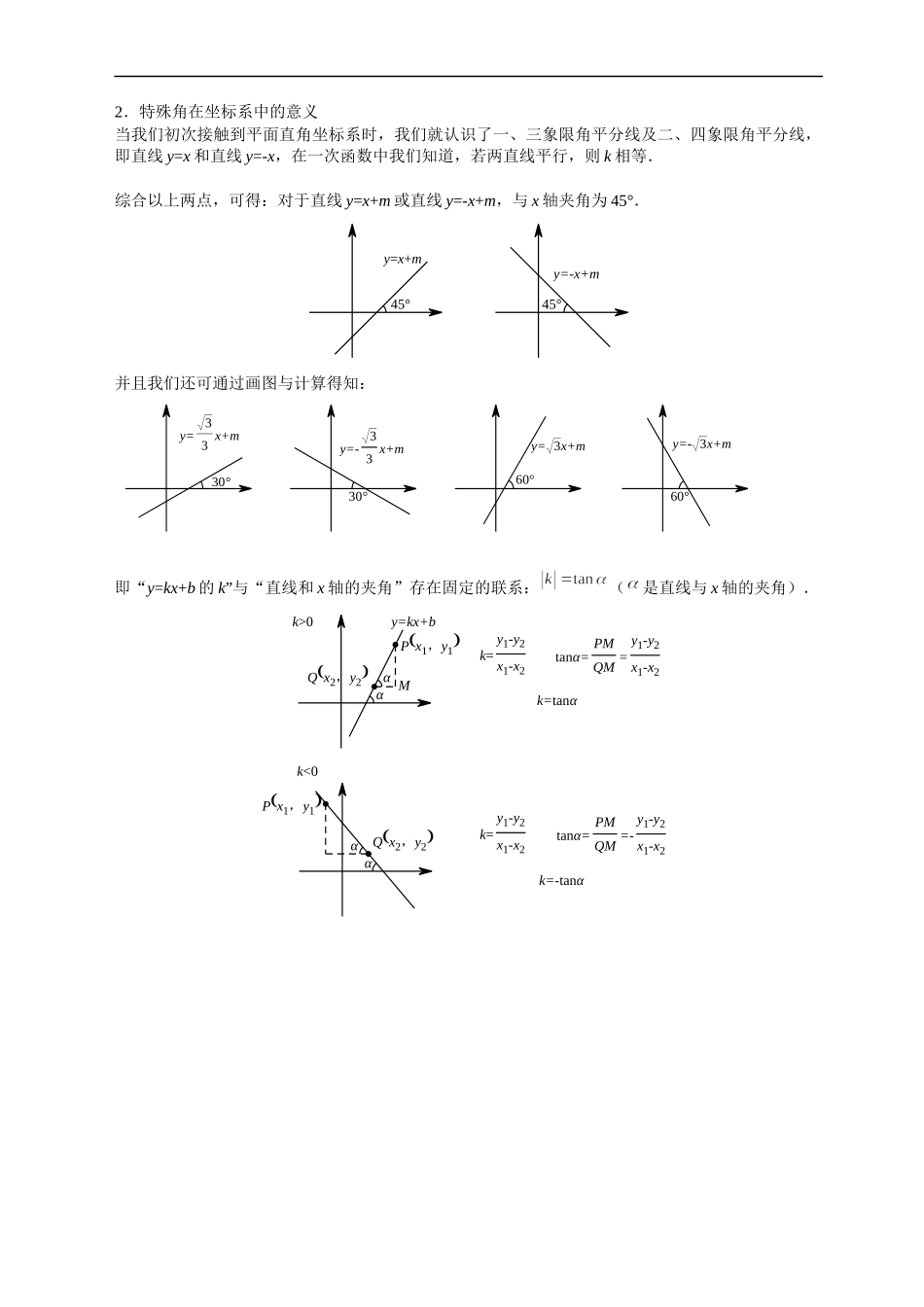
Section1特殊角的认识知识总结1.什么是特殊角?说到特殊角我们很快就能想到比如30°、45°、60°、90°等,事实上,之所以以上角能称为特殊角,关键在于这些角的三角函数值特殊,比如为什么我们会将60°称为特殊角,而50°便不是,原因很简单,,而我们并不知道50°的任一三角函数值.因此角度特殊不在于这个角是多少度,而在于其三角函数值是否有特殊值,所以除了常见的30°、45°、60°,我们可以扩充一下特殊角的范围.tanα+45°()=3tanβ+45°()=2α+45°β+45°3110β215α2tan2β=34tan2α=43α+β=45°2β2α55435βα三边之比为1:3:10tanβ=13β1013tanα=12α512三边之比为1:2:5三边之比为1:3:2cos60°=1213260°三边之比为1:1:2tan45°=145°11三边之比为1:3:2sin30°=1230°231第4讲二次函数中的特殊角问题2.特殊角在坐标系中的意义当我们初次接触到平面直角坐标系时,我们就认识了一、三象限角平分线及二、四象限角平分线,即直线y=x和直线y=-x,在一次函数中我们知道,若两直线平行,则k相等.综合以上两点,可得:对于直线y=x+m或直线y=-x+m,与x轴夹角为45°.y=-x+my=x+m45°45°并且我们还可通过画图与计算得知:y=-33x+my=-3x+my=3x+my=33x+m60°30°60°30°即“y=kx+b的k”与“直线和x轴的夹角”存在固定的联系:(是直线与x轴的夹角).k<0k>0k=y1-y2x1-x2tanα=PMQM=-y1-y2x1-x2k=-tanαPx1,y1()Qx2,y2()ααk=tanαtanα=PMQM=y1-y2x1-x2Mk=y1-y2x1-x2Qx2,y2()Px1,y1()y=kx+bαα3.坐标系中特殊角的处理在坐标系中构造定角,从其三角函数值着手:思路1:构造三垂直相似(或全等);思路2:通过三角函数值化“角度条件”为“直线k”.【引例】如图,在平面直线坐标系中,直线AB解析式为,点M(2,1)是直线AB上一点,将直线AB绕点M顺时针旋转45°得到直线CD,求CD解析式.MDCBAOyx45°经典例题【例1】如图,在平面直角坐标系中,一次函数y=2x-1的图像分别交x、y轴于点A、B,将直线AB绕点B顺时针旋转45°,交x轴于点C,则直线BC的函数表达式是_________.ABCOyx【例2】如图,直线y=x-3与坐标轴交于A、B两点,抛物线经过点B,与直线y=x-3交于点E(8,5),且与x轴交于C,D两点.(1)求抛物线的解析式;(2)抛物线上有一点M,当∠MBE=75°时,求点M的横坐标.EyxDCBAOSection2构造相等角知识总结问题:如何得到相等角?(1)平行:两直线平行,同位角、内错角相等;(2)角平分线:角平分线分的两个角相等...