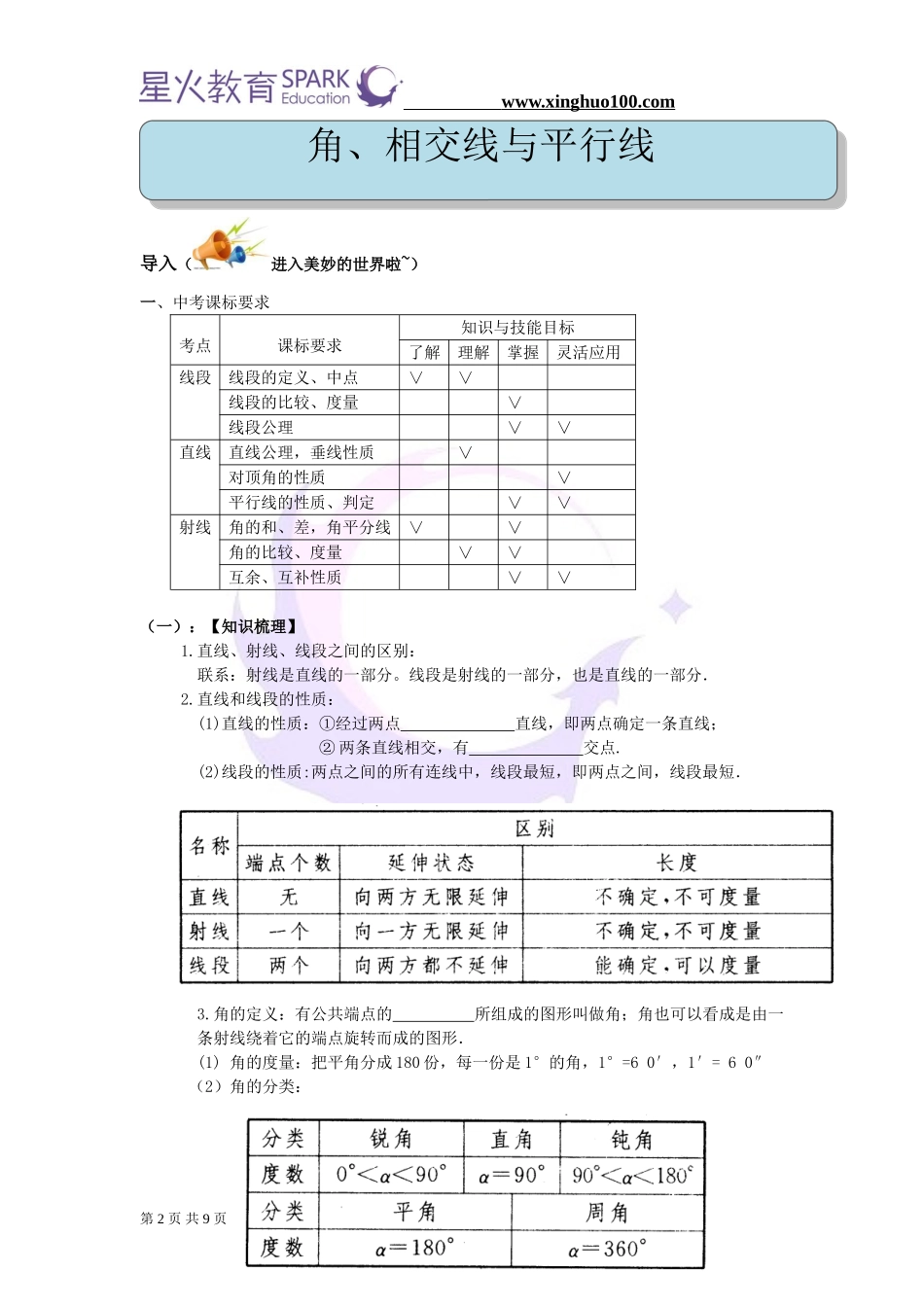
第1页共9页www.xinghuo100.com知人善教培养品质引发成长动力学生姓名性别年级学科数学授课教师上课时间第()次课课时:2课时教学课题教学目标了解角、相交线、平行线在中考的权重掌握角、相交线的应用以及平行线的判定、性质教学重点/难点重点:掌握直线、射线、线段的有关概念以及应用难点:正确区分概念及公理运用课后作业提交时间年月日学科组长检查签名:第2页共9页www.xinghuo100.com导入(进入美妙的世界啦~)一、中考课标要求考点课标要求知识与技能目标了解理解掌握灵活应用线段线段的定义、中点∨∨线段的比较、度量∨线段公理∨∨直线直线公理,垂线性质∨对顶角的性质∨平行线的性质、判定∨∨射线角的和、差,角平分线∨∨角的比较、度量∨∨互余、互补性质∨∨(一):【知识梳理】1.直线、射线、线段之间的区别:联系:射线是直线的一部分。线段是射线的一部分,也是直线的一部分.2.直线和线段的性质:(1)直线的性质:①经过两点直线,即两点确定一条直线;②两条直线相交,有交点.(2)线段的性质:两点之间的所有连线中,线段最短,即两点之间,线段最短.3.角的定义:有公共端点的所组成的图形叫做角;角也可以看成是由一条射线绕着它的端点旋转而成的图形.(1)角的度量:把平角分成180份,每一份是1°的角,1°=60′,1′=60″(2)角的分类:知人善教培养品质引发成长动力角、相交线与平行线角、相交线与平行线第3页共9页www.xinghuo100.com(3)相关的角及其性质:①余角:如果两个角的和是直角,那么称这两个角互为余角.②补角:如果两个角的和是平角,那么称这两个角互为补角.③对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.④互为余角的有关性质:①∠1+∠2=90°∠1、∠2互余;②同角或等角的余角相等,如果∠l十∠2=90○,∠1+∠3=90○,则∠2∠3.⑤互为补角的有关性质:①若∠A+∠B=180○∠A、∠B互补;②同角或等角的补角相等.如果∠A+∠C=180○,∠A+∠B=180°,则∠B∠C.⑥对顶角的性质:对顶角相等.(4)角平分线:从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.4.同一平面内两条直线的位置关系是:相交或平行5.“三线八角”的认识:三线八角指的是两条直线被第三条直线所截而成的八个角.正确认识这八个角要抓住:同位角即位置相同的角;内错角要抓住“内部,两旁”;同旁内角要抓住“内部、同旁”.6.平行线的性质:(1...